Az októberi Poli-Logi megfejtései

A Poli-Logi októberi megoldásai

1. Palindromok apraja-nagyja [2 pont]

Palindromszámoknak hívjuk azokat a pozitív egészeket, amelyeket visszafelé olvasva saját magukat kapjuk. (Ilyen számok például a 353 vagy a 7227.)

Mennyi a legnagyobb és a legkisebb háromjegyű palindromszám különbsége?

999-101=898

2. A Nagy Mester ajándéka [3 pont]

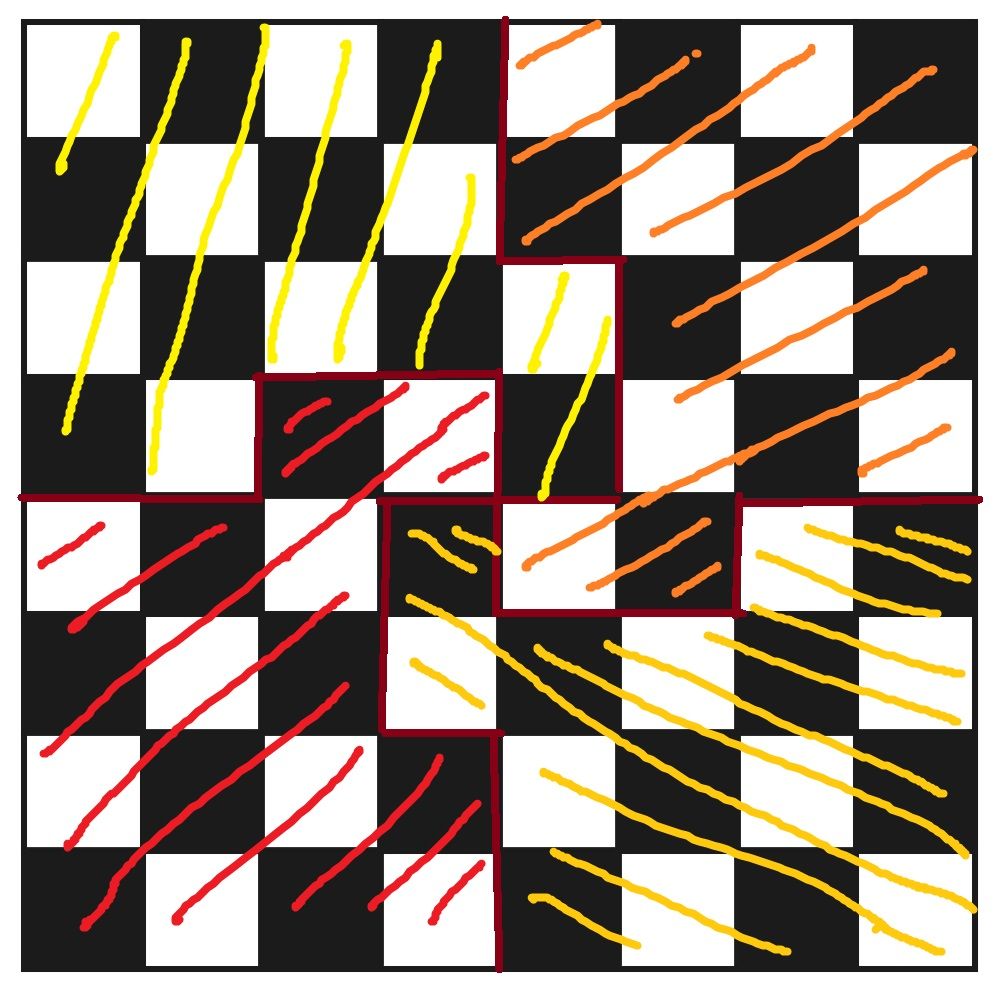
A sakk Nagy Mestere visszavonulni készül, és legendás, papiruszra festett sakktábláját szét akarja osztani négy legkiválóbb tanítvány között. Mind a négyüknek egy-egy tízszög alakú darabot szán, és mivel egyenlően nagyra becsüli őket, a négy darabnak ugyanolyan formájúnak és méretűnek kell lennie. És végül, a táblát csak a mezőket határoló élek mentén szabad szétvágni – ezt diktálja a Mester szépérzéke.

Segítsetek a Mesternek szétvágni a táblát négy egybevágó tízszögre!

Érdemes a sakktábla közepéből elkezdeni rajzolni a négy vágást, amelyek mind 4-4 töröttvonalból állnak, így végül négy tízszöget kapunk. Sok megoldás létezik. Az ábra ezek közül egyet mutat.

3. Alvó tengerészek [3 pont]

Egy hajó hálókörletén 10 tengerész alszik, akiknek az átlagéletkora 30 év. A kapitány egy villám dörrenésére felébred, és elindul körülnézni a fedélzeten. A tovább szundikáló 9 tengerész átlagéletkora így már csupán 28 év.

Hány éves a kapitány?

Az átlagokon és a kapitány életkorán nem változtat, ha föltesszük, hogy a matrózok mind egykorúak, 28 évesek. Mivel ők kilencen vannak, ezért a kapitány életkorát K-val jelölve azt kapjuk, hogy (9*28+K)/10=30. Ezt átrendezve kapjuk, hogy K=48, tehát a kapitány 48 éves.

4. A trapéz sötét oldala [3 pont]

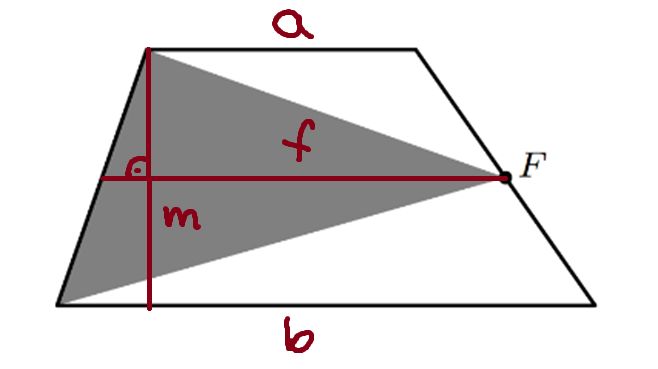
Az ábrán látható trapéz területe 20 cm³. F jelöli a jobb oldali szárának felezőpontját.

Mekkora a sötét rész területe?

A sötét rész területe éppen a trapéz fele, tehát 10 cm^3..
Jelöljük a trapéz alapjait a-val és b-vel, középvonalát f-fel, magasságát pedig m-mel. Egyrészt tudjuk, hogy f=(a+b)/2, illetve a trapéz területe (a+b)/2*m. Másrészt a sötét háromszögek összterületét megkaphatjuk mint f*m/2, ami éppen az előző kifejezés fele, használva az első összefüggést.

5. Garasoskodás [4 pont]

Bergengóciában egy kétes pénzügyi reform keretében a régi pénzt garasra cserélik. A Bergengóc Jegybank pedig kizárólag 6, 8 és 11 garasos érméket bocsájt forgalomba.

Melyik az a legnagyobb pénzösszeg, amit nem lehet visszaadás nélkül kifizetni ezekkel az érmékkel?

A megoldás 21.
Először is a 6-os és a 8-as érme segítségével minden 10-nél nagyobb páros szám kifizethető, de a 10 még éppen nem. Így aztán a páratlan összegek közül a 21 a legnagyobb, ami nem fizethető ki.

6. A mágikus M [4 pont]

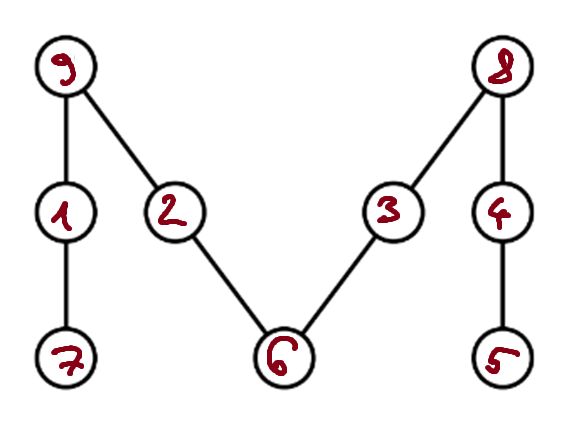
Az ábrán látható M forma akkor lesz mágikus, ha a kilenc mezejét kitöltjük az 1, 2, 3, …, 9 számokkal úgy, hogy mind a négy vonalon egyenlő legyen az oda tartozó három szám összege. Ezt az összeget az M mágikus erejének hívjuk.

Mennyi lesz a három kérdőjeles mezőbe írt szám összege, ha az M ereje a lehető legnagyobb?

A lehető legerősebb kitöltés érdekében a kérdőjelek helyére a lehető legnagyobb számokat szeretnénk írni. De kiderül, hogy ha a 7,8,9 számokat írjuk oda, akkor a négy vonal összege nem lehet egyenlő (4-gyel nem osztható az összeg). Viszont a 6,8,9 számokkal megoldható. Egy jó kitöltés látható az ábrán.