A POLI-LOGI márciusi fordulója
POLI-LOGI – Március
A megoldásaitokat a sandor.andras.m[kukac]gmail.com címre várjuk. Minden gondolatot fejtsetek ki, a végeredményre önmagában kevésbé vagyunk kíváncsiak. Nem kell az összes feladatot beküldeni, azon gondolkozzatok, ami tetszik!
Csapatban is gondolkozhattok bátran.
Azokat a résztvevőket, akik az év során legalább 40 pontot szereznek, csokijutalomban fogjuk részesíteni.
A beküldési határidő: 2021. április 12., hétfő
Jó gondolkodást!
- Erdei választások [3 pont]
Az erdőben demokratikusan akarják eldönteni, hogy ki a legokosabb állat. Az előválasztásokból a bagoly és a róka jutott a végső fordulóba. Minden állat egy-egy szavazatot adott le valamelyikükre. A szavazatszámlálásból kiderült, hogy a róka 14 szavazattal győzött.
A bagoly szeretné tudni, hogy legalább hány állatnak kellett volna megváltoztatni a szavazatát, hogy ő jöjjön ki győztesként.
- Kilences őrület [4 pont]
Gondoltam egy számra. Kivontam belőle 9-et, majd megszoroztam 9-cel. Eztán hozzáadtam 9-et és végül elosztottam 9-cel. Az eredmény 9 lett.
Melyik számra gondoltam az elején?
- Béna napfogó [5 pont]
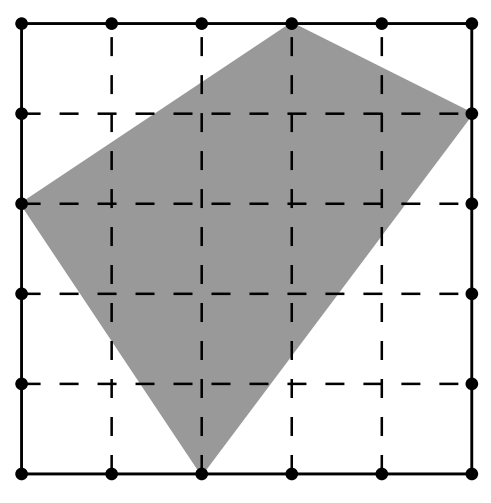
A kiskertem éppen négyzet alakú, oldalai 5 méteresek. A nyári napra készülve egy lepedőt próbálok kifeszíteni a kiskert fölé. Az ábrán látható módon sikerült, mert béna voltam.
Mekkora területet sikerült lefednem a kertből?
- Nárcisztikus szám [5 pont]
Van egy pozitív szám, aki csak saját magával szeret foglalkozni. Ezért összeszorozza a saját negyedét a saját felével, amire megkapja a saját négyszeresét.
Melyik ez a szám?
- Átlátszatlan üvegkocka [6 pont]
27 kis üvegkockából összeraktam egy 3x3x3-as nagy kockát. Ezen, bármelyik oldaláról is nézek rá, átlátok. Hány kis üvegkockát (és melyikeket) kell kicserélnem átlátszatlan kis fakockára, hogy a nagy kocka bármelyik oldaláról nézve 3×3 fakockát lássak?
- Sok kicsi kevésre megy [7 pont]
Egy kör mentén 99 szám áll, mindegyik +1 vagy -1. Tekintem az egymás mellett álló négyes csoportokat (ilyenből 99 darab van). Minden ilyen csoportról feljegyzem, hogy mennyi a négy szám szorzata. Majd a 99 így kapott szorzatot összeadom.
Mi a legkisebb összeg, amit így kaphatok?