A Poli-logi márciusi megfejtései

A márciusi Poli-Logi megfejtései

1. A gizai nagy piramis

A megoldás röviden: 

A piramis térfogata:	Vg ≈ 2,6⋅106 m3. Azaz kb. 2,6 millió köbméter.
A piramis felszíne:	Ag ≈ 1,4⋅105 m2. Azaz kb. 140 000 négyzetméter.
Az alaplap területe:	ta ≈ 5,4⋅104 m2. Azaz kb. 54 000 négyzetméter.
Oldallap területe:	to≈ 2,2⋅104 m2. Azaz kb. 22 000 négyzetméter.
Oldalél hossza:	o≈ 220,3 m.
Alapél-oldalél hajlásszöge:	α≈ 58,2°.
Oldalél-alaplap hajlásszöge:	β≈41,8°.
Oldallap-alaplap hajlásszöge:	γ≈51,6°.

Megjegyzés: Érdekesség, hogy az oldallap magassága (m_o≈187,15) és az alapél felének (a/2=116,2) aránya ≈1,61.
Ez az aranymetszési állandó értéke, amit Φ-vel szokás jelölni.
Másik érdekesség, hogy a piramis oldallapjának a területe (t_o≈ 21 746) és a gúla (m_g ≈146,7) magasságának a négyzete (21 521) nagyon közeli értékek. Tehát a Kheopsz piramis szerkezetében fellelhetők az ún. aranymetszés arányai.

 2. Sírfelirat

Diophantosz sírfeliratának megoldásában jelöljük valamilyen változóval, mondjuk „x”-szel a keresett életkort:
A szöveg szerint Diophantosz gyermekkora ​x//6​ évig, ifjúkora pedig, amikor szakálla kinőtt, ​x/12​ évig tartott. Esküvője ​x/7 ​év múlva volt, és gyermeke született 5 év múlva. Ez a gyermek ​x/2​ évig élt. Halála után még 4 évig élt az édesapa. Így a következő egyenletet lehet felírni:
​x/6+x/12+x/7+5+x/2+4=x​
Végigszorozva az egyenletet 84-gyel, az összevonásokat elvégezve 756=9x adódik. Tehát Diophantosz 84 évig élt.

3. Rejtélyes élet

Szczepan Jelenski „Pitagorasz nyomában” című könyvében szerepel ez a feladat.
A feladat kulcsa már mindjárt az első mondatban szerepel! Hogyan lehet az, hogy 44 éves kora után 1 évvel 100 éves lett? 44+1=45 lenne. A számokat vajon 10-es számrendszerben kell érteni? 44+1=100 csakis az 5-ös számrendszerben igaz!
Így tehát az egyetemet 44₅=4·5+5=24₁₀ éves korában fejezte be a fiatalember.
Az esküvője ezek szerint 100₅=1·5²+0·5¹+0·5⁰=25 éves korában történt, és a menyasszony 34₅=3·5+4=19₁₀ éves volt, a korkülönbség kettejük között pedig valóban 11₅=1·5+1=6₁₀ év volt.
Gyermekeik száma még 10-es számrendszerben is igen szép, hiszen 10₅=1·5+0=5₁₀ gyermek ma már igen ritka.
A 13000₅ zloty kereset 1·5⁴+3·5³+0·5²+0·5¹+0·5⁰=625+3·125=1000₁₀ zloty az akkori években talán tényleg elég lehetett.
Mennyi pénzt adott vajon a testvérének? Az 1/10₅=1·5^-1=1/5-öd rész 200₁₀ zloty-t ér.
Így kettejüknek 11200₅=1·5⁴+1·5³+2·5²+0·5¹+0·5⁰=625+1·125+2·25=800₁₀ zloty maradt havonta.

4. Aranyos arányos

Két természetes szám aránya 3:1. A két szám négyzetösszegének és összegének aránya 5:1. Melyik ez a két szám?
Megoldás: 6 és 2

 5. Holdacskák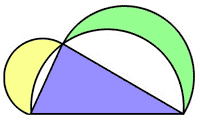

Hippokratész ókori görög matematikus sokat foglalkozott körívek és egyenesek által határolt síkidomok területének meghatározásával. A most következő példa – Hippokratész „holdacskái” – egy konkrét példa arra, hogy görbe vonalakkal határolt síkidom négyszögesíthető.
A holdak területét megkapjuk, ha a befogók fölé emelt félkörök területéből kivonjuk azoknak a körszeleteknek a területét, amelyeket úgy kapunk, hogy az átfogó fölé emelt félkör területéből kivonjuk a háromszög területét.

Formulával: Jelöljük a derékszögű háromszög befogóit „a” és „b”, az átfogót pedig „c” változóval. Ekkor a derékszögű háromszög területe: ab / 2, a befogók fölé emelt félkörök területe:
(a/2)² x p /2 és (b/2)² x p /2.
Az átfogó fölé emelt félkör területe: (c/2)² x p /2.
Így a körszeletek területe: (c / 2)² x p / 2 – ab / 2.

Holdak területe tehát = (a / 2)² x p / 2 + (b/2)² x p / 2 – [(c/2)² x p / 2 – ab / 2].
Zárójelek felbontása után: a²p /4 + a²p /4 – c²p /4 + ab / 2.
Emeljük ki p / 4-t, így p / 4(a² + b² – c²) + ab / 2
A zárójelben szereplő kifejezés Pitagorasz tétele értelmében nullával egyenlő, ezért a holdacskák területe = ab / 2. És ezt kellett igazolni.

6. Tökéletesek

A püthagoreusoktól származik a tökéletes szám fogalma. Ilyenek azok a természetes számok, amelyek egyenlők osztóik összegével, az egyet is beleszámítva, de magát a számot nem. Igazold, hogy a 496 és 8128 tökéletes számok!

Megoldás:
496 = 1+2+4+8+16+31+62+124+248 (Ezek 496 osztói, a 496 kivételével)
8128 = 1+2+4+8+16+32+64+127+254+508+1016+2032+4064 (Ezek 8128 osztói, a 8128 kivételével)