A novemberi Poli-Logi megoldásai
Poli-Logi
Novemberi megoldások
1. Dávid háromszögei [4 pont]

Hány háromszöget határolnak az ábra vonalai?
Vigyázz, ne hagyj ki egyet se!
Csak szabályos háromszögek vannak. A kicsi, 1 méretűből 12 darab van, a közepesből 6, a nagyból pedig 2. Ez összesen 20 darab.
2. Fodrászlábak [4 pont]
Egy fodrászüzletben a vendégeknek kényelmes négylábú karosszékek vannak kirakva, a fodrászok pedig háromlábú hokedliket használnak. Éppen minden széken ül valaki (és senki nem áll) amikor összesen 34 lábat tudunk megszámolni. Hányan vannak az üzletben?
A rajtuk ülőkkel együtt a székek 5, illetve 6 lábat adnak. A 34 csak egyféleképpen áll elő ötösök és hatosok összegeként: 34=2*5+4*6. Tehát hatan vannak az üzletben, két fodrász és négy vendég.
3. Békés futók [5 pont]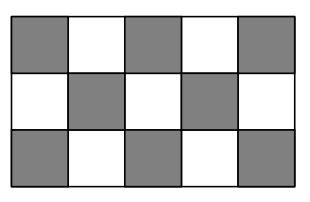
A mellékelt sakktábla-részre úgy szeretnék futókat föltenni, hogy egyik se üsse a másikat. Legföljebb hányat tudok így föltenni?
A fehér mezőkre legfüljebb 3 futó kerülhet, a feketékre pedig maximum 4, összesen tehát 7.
4. Hónap-rejtély [4 pont]
A fiókban találtunk egy régi naptárat áprilisnál kinyitva. Azt vesszük észre, hogy ebben a hónapban hétfőből, szerdából és szombatból is éppen négy van. Milyen napra esik a hónap utolsó vasárnapja?
A harmincnapos áprilisban csak úgy lehet a fenti napokból pont 4-4, ha elseje csütörtökre esik. Így az utolsó vasárnap 25-re esik.
5. Rendszerető kilométerkövek [6 pont]
A Rácegres és Pácegres közötti országúton kilométerenként vannak jelzőkövek. Mindegyik kő két oldalára rá van írva, hogy onnan milyen messze van az egyik, illetve a másik falu, kilométerben mérve – csupa egész szám. Minden kövön a ráírt számjegyek összege 13. Hány kilométerre van egymástól Rácegres és Pácegres?
Csak úgy nem változik a számjegyösszeg a tízesátlépéseknél, ha a két falu távolsága (tehát a számpárok összege) 9-re végződik. Innen könnyedén látszik, hogy a távolság 49 kilométer kell, hogy legyen.
6. Sokszögbe gabalyodva [7 pont]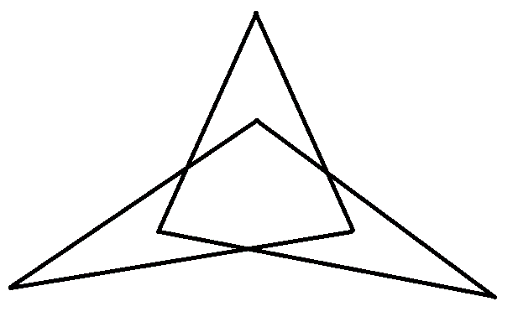
Rajzolj egy olyan hurkolt sokszöget, aminek minden oldala pontosan egy másik oldalát metszi, és semelyik oldal nem megy át a végeitől különböző csúcson. Minél kevesebb oldalú sokszöget rajzolsz, annál több pontot kapsz.
Csak páros sokszög tudja a fenti módon metszeni magát. Négyszög nincs ilyen, viszont hatszög igen. Például:
Megfejtő: Gyenes Bertold (Anonym).
Az 1., a 2. és a 4. feladatra hibátlan megoldást küldött be.
Gratula