A januári POLI-LOGI megoldásai
POLI-LOGI – Január
Megoldások
- Sárkányfogak [4 pont]
Sárkányvárosban 8 sárkány él. Rendre 1,2, … 8 fejük van. Minden sárkánynak meg vannak számozva a fejei 1-től addig, ahány feje van. Minden ilyen fejnek éppen annyi foga van, ahányas a száma.
Hány sárkányfog van összesen Sárkányvárosban?
Készítsünk el egy táblázatot, amelyben szerepel a sárkányok fejeinek száma, illetve a fogaik száma.
|
A sárkány fejeinek száma |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
A sárkány fogainak száma |
1 |
3 |
6 |
10 |
15 |
21 |
28 |
36 |
Minden sárkánynak épp annyival van több foga a sorban előtte állóénak, amennyi az utolsó fejének sorszáma. Így a táblázat második sorát úgy lehet könnyen kitölteni, ha a megfelelő fejszámot hozzáadjuk az előző sárkány fogszámához.
A nyolc sárkány együttes fogszámát pedig úgy kapjuk meg, hogy összeadjuk a táblázat második sorának elemeit. Ez az összeg pedig 120.
- A kis pók nagy túrája [6 pont]
Egy kis pók az ábrán látható kocka A-val jelölt csúcsában lakik. Szeretne körutazást tenni a kockán, melynek során az összes csúcsot bejárja. A pók csak a kocka élein hajlandó közlekedni és egy élen épp egy óra alatt ér végig. A nagy út végén otthon szeretne végezni.
Legalább hány órára van szüksége egy ilyen körutazáshoz?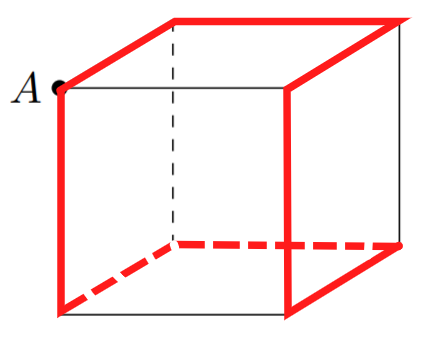
A pók 8 óra alatt körbejárhatja a kocka összes csúcsát. Ezt többféleképpen teheti meg, egy lehetséges körsétát mutat az ábra.
Azt is beláthatjuk, hogy ennél kevesebb idő semmiképp nem elég. Bármelyik csúcsból indulva egy új csúcsba eljutni legalább egy órába telik, így a 7 új csúcs meglátogatása, illetve a hazatérés együtt legalább 8 órát tesz ki.
- Házfestés [5 pont]
Van egy háromemeletes ház, amelyet három színnel szeretnénk festeni: pirossal, kékkel és zölddel. (Nem muszáj az összes színt felhasználni). Egy-egy emeletet egyszínűre szeretnénk festeni, de – hogy ne legyen túl unalmas – a szomszédos emeleteket különböző színűnek akarunk.
Hányféleképpen festhetjük ki a házat ezekkel a feltételekkel?
Haladjunk gondolatban lentről fölfelé. A legalsó emeletet a 3 szín bármelyikére festhetjük. Ezután a másodikat már csak kétféle színűre, mert nem lehet ugyanolyan, mint az első. Hasonlóképpen a harmadiknál is két szín közül választhatunk. Így e három szám szorzataként megkapjuk, hogy 12 féleképpen festhetjük ki a házat.
- Pídarabolás [6 pont]
Az első ábrán egy görög π betűt formájú sokszög látható. Ezt felvágtuk néhány darabra és megszámoztuk a darabokat. Ezekből ki lehet rakni egy négyzetet. A kirakást elkezdtük a második ábrán.
Mennyi lesz a szürke négyzetbe belemetsző darabok sorszámainak összege?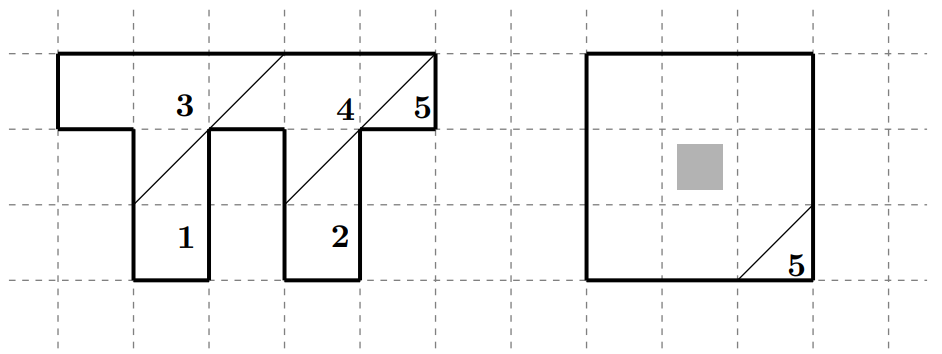
A darabok lerakását a legnagyobb méretű 3-assal érdemes kezdeni. Ennek a felső éle 3 egység hosszú, épp, mint a négyzet oldala. Könnyű meggyőződni róla, hogy ha ezt az élet nem illesztjük a négyzet egyik oldalára, akkor nem fér el a többi darab. Az illesztéshez pedig két szabad él jöhet szóba, a felső és a bal oldali. Mindkét esetben egyértelműen folytathatjuk a lerakást, és az egyik esetben sikeresen el is fognak férni a darabok. (E két esetet láthatjuk az ábrákon.)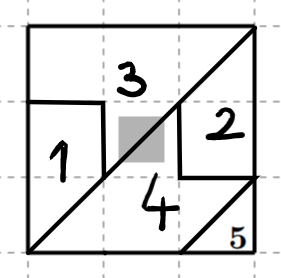
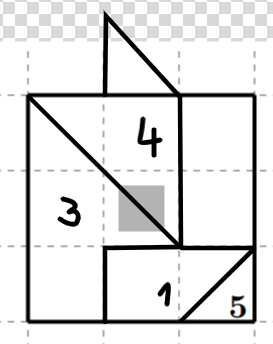
Leolvashatjuk, hogy az egyetlen helyes kitöltésnél a keresett összeg 7. (Az 1-es és a 2-es darab egybevágó, így felcserélhető, de ez nem változtat az összegen.)
- Nagy-nagy szám [7 pont]
Választottunk egy természetes számot és ezt 10-szer leírtuk egy papírra. Ezt a 10 számot összeszoroztuk és 282 475 249-et kaptunk.
Melyik számból indultunk?
(Itt különösen fontos az indoklás – az nem ér, hogy „számológéppel kipróbáltam”.)
Először érdemes észlelni a szám nagyságrendjét: ez egy kilencjegyű szám, tehát a tíz tizedik hatványánál kisebb. Így a kiindulási számunk kisebb, mint 10. Ezután érdemes megjegyezni, hogy a nagy számunk páratlan, tehát nem lehet páros szám, amiből indultunk. Sőt, öttel és hárommal sem osztható – utóbbit ellenőrizhetjük a számjegyösszeg (43) 3-as osztásával. Így viszont azt kapjuk, hogy a kiindulási számunk csak a 7 vagy az 1 lehet, ahol ez utóbbi nyilván 1-et ad magával 10-szer összeszorozva. Egy számológéppel könnyen ellenőrizhetjük, hogy 10 darab 7-es szorzata épp a megadott szám.
Megfejtő: Gyenes Bertold (Anonym).
Hajrá!